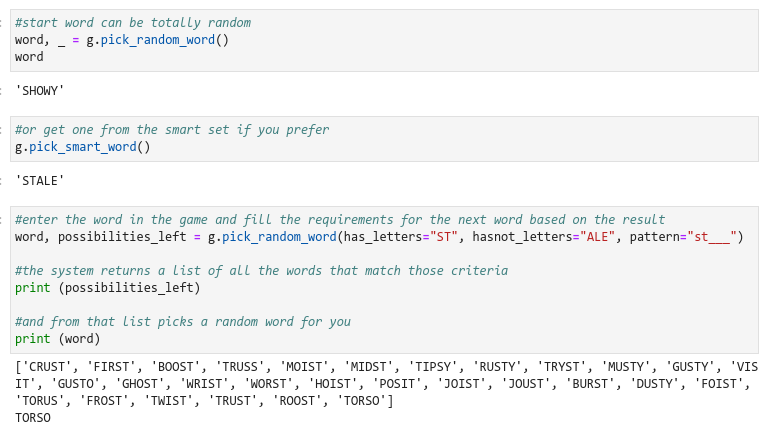
What is the best Wordle strategy?
Wordle is a rather popular online code-breaking game that works as a words-based version of the old Mastermind game. If you do not know what wordle is, you may want to read this nice overview of the game and its success published in the Guardian. If you do know what Wordle is then you have probably wondered whether there is a perfect strategy to play it. I wondered the same and dedicated a Sunday evening of my time to run some experimental analysis which I like to share with the wordle world.
The first step was to collect a dictionary of all the five letters words in English. Every day, the wordle javascript picks a word from a list of 2315 words (and accepts further 10657 words as possible entries). A more comprehensive list of 3450 words can be found here.
I then coded a wordle solver: a piece of software that will get the computer to play wordle against itself so that we can run hundreds of thousands of iterations and do some stats (here is a sample notebook on how to use it). The first thing to check is to calculate the null hypothesis: how successful would we be if we were to try and solve the puzzle using completely random words at every attempt? The answer, based on a Montecarlo repeat of 100k games, is 0.25%. That means we would fail 99.75% of the time. We can certainly do better than that!

We can now go and evaluate different strategies. I am not going to take a brute-force approach for this problem but rather a hypothesis drive one, listing strategies that I believe real users are considering. I evaluate two variables in the strategy: the first variable is whether it makes sense to start with a “smart word”, that is a word that contains a pondered amount of carefully selected letters. For instance, we may want to start with words that contain the most frequently used letters in the list. Analyzing the letter frequency in all the 2315 wordle words, we come down with the following values:
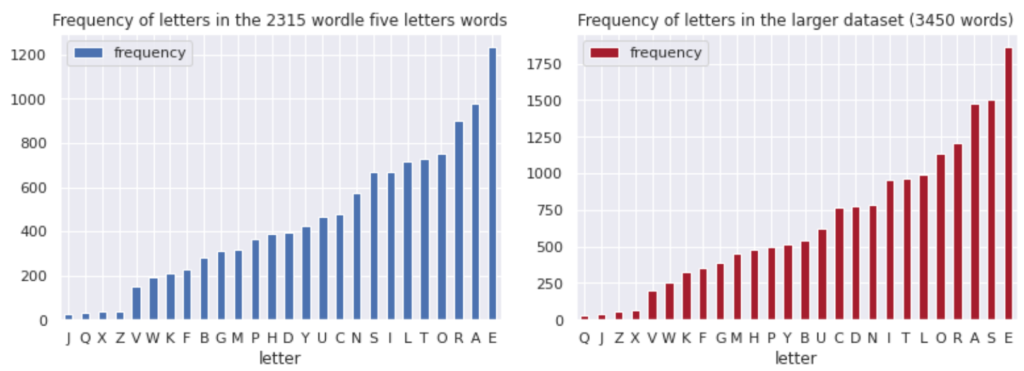
We can now come up with a list of word that uses the most frequent letters, excluding of course words that have double letters inside. The first 20 words in the list for the wordle dataset would be the following ones:
['LATER', 'ALTER', 'ALERT', 'AROSE', 'IRATE', 'STARE', 'ARISE', 'RAISE', 'LEARN', 'RENAL', 'SNARE', 'SANER', 'STALE', 'SLATE', 'STEAL', 'LEAST', 'REACT', 'CRATE', 'TRACE', 'CATER', 'CLEAR', 'STORE', 'LOSER', 'AISLE', 'ATONE', 'TEARY', 'ALONE', 'ADORE', 'SCARE', 'LAYER', 'RELAY', 'EARLY', 'LEANT', 'TREAD', 'TRADE', 'OPERA', 'HEART', 'HATER', 'EARTH', 'TAPER', 'PALER', 'PEARL', 'TENOR', 'ALIEN', 'AIDER', 'SHARE', 'SHEAR', 'CRANE', 'TAMER', 'GREAT']Some of these words actually have the same valence given that they are anagrams of each other but the list provides some sensible starting point for what I will be calling the “smart start strategy”. The alternative to a smart strategy is to be using a random word every time.
The second variable in our strategic considerations is whether it makes sense to use exclusion words. Exclusion words are words that do not contain letters that we have already tested. They allow us to learn more about which letters are or are not present in the final word. For instance, in the two examples below we use a smart word start and then an exclusion word next which not only ignores but actually avoids all the letters used in the first attempt, even when successful. This allows us to learn more about which letters we should be using.

An exclusion strategy could be used for attempts number 2 and attempt number 3 in principle, like in the two examples below:

Obviously, the drawback of using an exclusion strategy is that we are not going to be able to guess the word because we are purposely excluding the letters we know are in the final word!
There are other aspects of the strategy that we should be using that we could in principle test: for instance, when should we start using words with double letters? If we take the smart word start, I believe we should exclude words with double letters and the same of course apply with the exclusion strategy too. So, all in all we can now compare four different strategies:
| Strategy | Use Smart Start? | Exclusion words |
| 1 | NO | NO |
| 2 | YES | NO |
| 3 | YES | 1 |
| 4 | YES | 2 |
We run a Montecarlo simulation of all four strategies, setting 1000 games each and we find the following performance per strategy
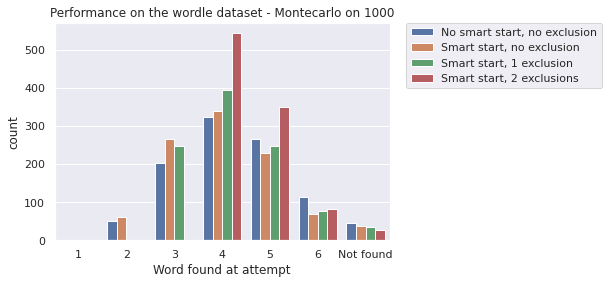
average success attempt: 4.322 4.09 4.09 4.263
All strategies perform very well overall, with a success rate above 95%. The distribution of successful attempts is gaussian as expected, with a peak at attempt 4. Obviously, any exclusion strategy will preclude the possibility to guess the word at attempts number 2. So the take-home message is the following: if we want to maximize the probability of finding the word we should use strategy number #4 which gives us the highest success rate of 97%. However, that high success rate comes at the expense of renouncing the possibility of finding a guess at attempts 1-3. If we want to maximize early successful attempts (at the expense of success rate) we should go for strategies 2 or 3.
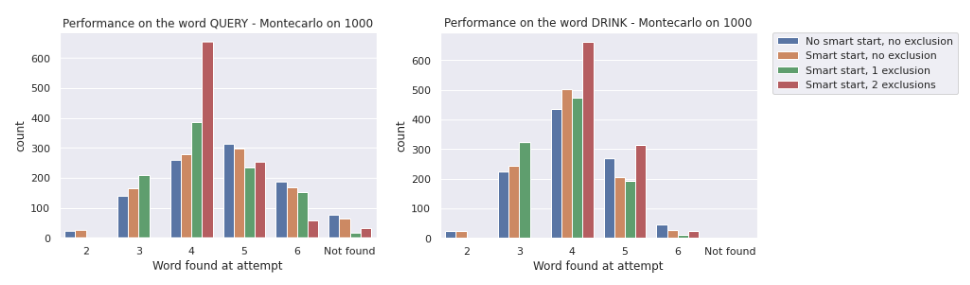
Interestingly enough, the system can also be used to evaluate how difficult a word is. For instance, in the example below we try to solve the word QUERY (left) or DRINK (right)
To solve the daily wordle